Qual o fator de aumento de uma câmera ?

[jsmoraes]

É comum compararmos a imagem de uma câmera ou webcam com a imagem de uma ocular, e atribuir as câmeras o mesmo fator de aumento da ocular.

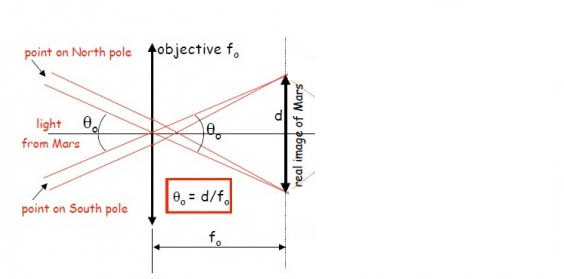
Falsa interpretação dos fatos ! Uma câmera não aumenta a imagem. Ela não é uma lente. A resolução proporcionada pelo tamanho dos pixels e o FOV que a diagonal do sensor proporciona é que dão esta falsa impressão de aumento.

Eis um resumo das postagens sobre o assunto, retirado do Cosmoforum - tópico: astrofotografia > astrofotografia CCD > WebCam > Cálculo da distancia focal de uma webcam

postagem de VitorAD:

O que é o aumento de um telescópio?

Ele é resultante de dois ângulos. O ângulo aparente da imagem projetada lá do infinito no plano focal da objetiva (Theta o) e do ângulo aparente desta imagem projetada pela ocular nos nossos olhos (Theta), o que podemos traduzir por:

M = tg(Thetao)/tg(Theta)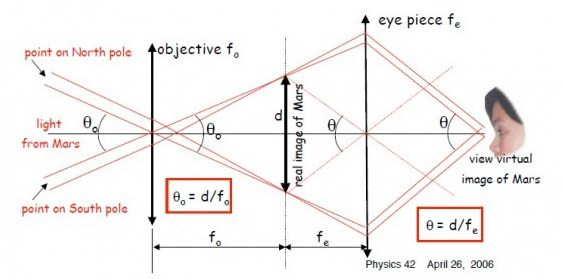



Óbvio que a partir disto podemos chegar nas equações clássicas do aumento como:

M = Dist. Focal Objetiva / Dist. Focal Ocular = Fo / Fe
M = AFOV / TFOV, etc...

Porém, o que é o aumento de um chip? O chip é por acaso uma lente que altere ângulos das imagens? Não, não é mesmo?

Mas vamos pensar por outro lado. Pensemos na Lua. Ela possui um diâmetro aparente de 0,5 graus no céu. Qual é o seu tamanho projetado sobre a superfície plana de um chip em uma objetiva de 1000 mm de distância focal?

Da figura acima vemos que o tamanho da imagem projetada d é igual ao angulo aparente da imagem (em radianos) multiplicado pela distância focal da objetiva, ou:

d = 1000 mm x 0,5 graus x pi / 180 graus = 8,7 mm.

Bom, daí eu já concluo que o chip não aumenta nada não é mesmo? Se eu colocar um chip de 1/4 ou um chip de 1/2 o tamanho da Lua em cada um vai ser de aproximadamente 9 mm pois depende apenas da distância focal do telescópio. Não tem nenhuma ocular para magnificar este tamanho! O chip não passa de uma face plana colocada neste plano focal.

Mas já consigo perceber algumas coisas. No meu chip de 1/4 que possui 4,5 mm de diagonal a Lua não cabe toda e no de 1/2 que tem 8 mm de diagonal ela quase cabe toda!

Hum...Será então que o chip de 1/4 aumenta mais que o de 1/2? Sigamos em frente.

Como um chip enxerga? Ele é composto de várias células sensitivas chamadas pixels que possuem um tamanho especifico.

Imaginemos que o chip tenha os pixels quadrados com tamanho de 5 mícrons ou 0,005 mm. Digamos que o chip de 1/4 tenha um formato quadrado de 3,35 mm x 3 mm com área de 10 mm2 e que o chip de 1/2 tenha um formato de 6,25 mm x 5 mm ou 31,25 mm2.

Como nossa célula ou pixel tem uma área de 0,005 mm x 0,005 mm ou 0,000025 mm2 nos dois chips temos que o chip de 1/4 possui 10 / 0,000025 ou 400.000 pixels (0,4 Megapixels) e no de 1/2 temos 31,25 / 0,000025 ou 1.250.000 pixels (1,25 Megapixel).

Alguma conclusão? Se cada pixel de cada câmera enxerga o mesmo tamanho da Lua pois ambos possuem 5 milésimos de mm, elas ampliam a imagem diferente? Não! Apenas o tamanho do campo da imagem é diferente! Ou seja, o FOV! É como se fossem duas oculares de mesma distância focal com AFOVs diferentes. Há mais pixels no chip de 1/2 para enxergar mais partes da Lua com o mesmo tamanho. Simples assim e a Lua continua tendo os mesmos 9 mm em cada chip.

Não tem como comparar aumentos por oculares e aumento em chip pois este não existe.

postagem de lhvilatur e resposta de VitorAD:

lhvilatur:
1 - quando digo que uma SPC equivale aproximadamente a uma ocular 4,5, na verdade é o campo de visão que se equivale. Se com esta ocular eu só vejo uma cratera da Lua, a SPC também só verá uma cratera da Lua.

VitorAD:
Não. Quando você falar que a SPC equivale a uma ocular de 4,5 mm você tem que referenciar que esta ocular possui como AFOV o número mágico citado por parsec de aproximadamente 50 graus.

Para para pensar. Você possui duas oculares de 4,5 mm. Uma com AFOV 50 graus e outra com AFOV 80 graus. Em nosso telescópio de 1000 mm de DF ambas vão magnificar 222x, correto?

Porém o campo real é o AFOV / M.

A de 50o possui um campo real de 50 / 222 ou 0,225 graus e a outra 80 / 222 ou 0,36 graus. Obviamente na ocular de maior campo eu verei mais do que apenas aquela cratera...

Como é que os caras chegaram a esta comparação esdrúxula.

O maior campo que o chip abrange é o de sua diagonal.

Sabemos que o TFOV do chip em graus é dado pela relação
TFOV = 57,3 x diagonal (mm) / DF (mm) (I)

Ora, das equações clássicas, sabemos que o aumento M é dado por:
M = AFOV / TFOV (II)
e
M = DF / Do (i)

Das equações (II) e (i) podemos rearrumar e escrever que TFOV é:
TFOV = AFOV x Do / DF (IV)

Se compararmos agora (I) com (IV) vemos que:
Do (mm) = 57,3 x Diagonal (mm) / AFOV (graus)

Para que eu possa dizer que os aumentos são "equivalentes" eu precisaria observar a imagem da tela e a do telescópio com uma ocular Do com a distância focal do tamanho da Diagonal mas com 57,3 graus AFOV.
 Sacou?

lhvilaltur:
2 - Nas fotos as imagens aparentam ter maior ampliação, não por ampliação real, mas por serem digitais permitem ampliação digital. Ou numa comparação vulgar: em uma TV de 42 polegadas a imagem é maior do que uma de 14 polegadas por afastamento espacial entre os pixeis (pontos luminosos da imagem). Daí que em se aproximando desta grande TV, vemos seus pixeis individuais. Já na de 14 pol. é necessário uma aproximação bem maior para ver seus pixeis.

A a resolução só afetaria na qualidade, detalhes e nitidez da imagem, pois seriam mais pontos luminosos (pixels) na montagem da imagem digital.

É isto mesmo, Vitor ou viajei ?

VitorAD:
Eu não sei se viajou mas eu viajei
 
Do nosso exemplo da Lua lá atrás já vimos que o tamanho da diagonal ou do chip é o que determina o campo real da imagem abarcado pelo chip, certo?

Resolução é a capacidade de separamos coisas, ou enxergarmos coisas menores.

Pensando naquele exemplo com uma objetiva de 1000 mm de DF, mas agora pensemos em dois chips com o mesmo tamanho de diagonal. Um com pixel de 10 mícrons e outro com pixel de 5 mícrons.

Vamos brincar diferente. A Lua tem um diâmetro equatorial de 3.476 Km. Em nosso telescópio de 1000 mm, ela tem um diâmetro de 9 mm no plano focal. Ou seja, cada mm corresponde a 3476 / 9 ou 386,2 Km.
Como o pixel de 10 mícrons enxerga 0,01 mm e o de 5 mícrons enxerga 0,005 mm podemos dizer que o pixel de 10 enxerga detalhes de 386,2 x 0,01 ou 3,8 Km e o de 5 enxerga detalhes de 1,9 Km.

Interessante não? Ambos os chips tem o mesmo tamanho de diagonal, enxergam o mesmo campo da Lua, porém o de pixel menor consegue identificar mais detalhes menores na superfície lunar que o outro.

Agora vem o desafio. Se a resolução do chip depende apenas da distância focal do telescópio e do tamanho do seu pixel, por que eu não consigo ver o mesmo número de detalhes em um refrator 60 mm F=1000 mm e em um newtoniano 200 mm F/5 de mesma distância focal? Se eu estou usando a mesma câmera eu não deveria ver os mesmos detalhes?

Postagem de Parsec:

...essa confusão de se atribuir o aumento em função da diagonal do chip é oriunda da fotografia convencional e deve-se ao fato do camarada não continuar lendo o que os caras dizem.

Quando você coloca uma lente de 50 mm numa câmera com um sensor full frame, ou um filme 35 mm (24 mm x 36 mm), dai o nome "full frame", a diagonal mede 43.27 mm

Uma lente 50 mm esta próximo desse valor e produz um campo de visão com 47 graus, o que chega bem perto do valor de 53 graus que é aproximadamente o campo de visão humano

Devido a isso se chama a lente de 50 mm como "lente normal" e como ela tem aproximadamente o mesmo valor nominal da diagonal do sensor full frame, vem toda essa confusão.

Se utilizarmos uma lente com distância focal de 11.7 mm em um sensor com tamanho de 8.10 x 6.08 mm, como a diagonal do CCD vai medir 10.13 mm, novamente teremos uma lente produzindo uma imagem de 47 graus de campo e esta será uma "lente normal".

Naturalmente para o pessoal da fotografia não ficar confuso, eles utilizam um termo chamado de lente equivalente.

No mais, os cálculos aplicados ao processo de ampliação em astrofotografia são os já esplanados pelo Vitor acima. Observem que o tamanho do pixel e a área coberta por estes são de importância. Em geral se determina uma câmera em função do telescópio que será utilizada. Em outras palavras, nem sempre a mesma câmera pode ser utilizada em qualquer telescópio

Postagem de VitorAD:

O limite de resolução de Dawes fala que o poder de resolução de um telescópio em segundos de arco é função da abertura da objetiva e obtido pela equação p (") = 116 / D (mm).

Para o seu newtoniano de 203 mm ele é de 116 / 203 ou 0,57 segundos de arco. Ou seja seu telescópio consegue separar teóricamente dois discos de Airy separados em 0,57" . Para o 305 mm ele é de 0,3770
Não vou aqui discutir se o Limite de Dawes é ou não é o melhor meio de sabermos o poder de resolução, mesmo porque os astrofotógrafos frequentemente ultrapassam este limite devido a influência da função da diferença de contraste entre os dois pontos separados. Para todos os efeitos estamos discutindo uma abordagem inicial, um ponto de partida de onde experimentaremos com o nosso setup.

O Teorema de Nyquist fala que para amostrarmos todo o poder de resolução de nosso telescópio, devem ser utilizados no mínimo 2 pixels. Se usarmos apenas um ocorrerá perda de informação. Ou seja, a resolução ideal que procuramos para nossa câmera em pixels deve ser a metade da resolução teórica.

Se seu telescópio separa 0,57", procuramos uma resolução na câmera de 0,57" / 2 pixels ou 0,28 segundos de arco / pixel. No 305 mm seria de 0,3770/2 = 0,1885

Mas a sua câmera possui o tamanho do pixel fixo. Sendo uma SPC ele é de 5,6 mícrons ou 0,0056 mm.

Teremos que ajustar a distância focal para obter esta resolução. Para isto utilizamos a equação para resolução do chip:
S ("/px) = 206.265 x tamanho do pixel (mm) / Distância Focal (mm)

Como nossa resolução S é de 0,28 "/px e o pixel é de 0,0056 mm, descobrimos que precisamos de uma distância focal equivalente de:
F (mm) = 206.265 x 0,0056 / 0,28 ou a distância focal deve ser de 4.125 mm aproximadamente, o que daria uns F/20 a F/21.

Para o 305 mm seria: 206.265 x 0,0062 / 0,1885 = 6784 mm -> f/22

Você precisaria de uma Barlow 4X ou projeção com ocular.
Para o 305 mm : idem

Mas qual ocular utilizar?

A distância focal equivalente por projeção ocular é:
Feq (mm) = F (mm) x distância da ocular ao chip (mm) / distância focal da ocular (mm)

Se arrumarmos a coisa toda, neste cenário, precisamos que a distância da ocular ao chip seja 4 vezes a distância focal da ocular.

Se você usar a de 10 mm coloque o chip a 40 mm. Se for a de 6,5 a 26 mm. A de 4 é inutilizável pois vai ficar muito próximo e acabar batendo em alguma coisa.

-----

A QC4000 tem o mesmo pixel size da SPC. 5,6 mícrons e uma diagonal de 4,5 mm.

O meu laptop com tela com diagonal de 14 polegadas com resolução de 1280 x 800 possui o tamanho horizontal de 0,8 vezes a diagonal, ou seja 304,8 mm. Como ela tem resolução horizontal de 1280 pixels, cada pixel mede 304,8 / 1280 ou 0,238 mm.

Então meu laptop amplia a imagem da câmera em 0,238 mm / 0,0056 mm, ou 45,2 x.

-------------

TFOV = 57,3 x diagonal (mm) / DF (mm)

De onde vem ou a que se refere este 57,3 ?

Da matemática. Estamos utilizando ângulos em radianos para podermos comparar quantidades diferentes mas de mesma dimensão.

Um círculo tem 2 x Pi radianos que é igual a 360 graus. Logo 1 radiano = 180 / pi = 57,3 graus ou 3438 minutos ou 206265 segundos.

De Jorge (lhvilatur):
Ao se utilizar uma barlow,  um extensor entre barlow e câmera proporciona um acréscimo na RESOLUÇÃO da imagem, e não AUMENTO.

[jsmoraes]

Gráfico quando somente câmera com projeção direta: